‘
反向传播是现代神经网络训练的重要组成部分,使得这些复杂的算法能够从训练数据集中学习并随着时间的推移不断改进。
‘
理解和掌握反向传播算法对于神经网络和深度学习领域的任何人来说都是至关重要的。本教程将深入探讨反向传播。
它首先解释了什么是反向传播以及它是如何工作的,以及它的优点和局限性,然后深入实践应用到一个广泛使用的数据集中。
什么是反向传播?
反向传播算法是在1970年代引入的,它是一种根据上一次迭代或时期中获得的误差率来微调神经网络权重的方法,这是训练人工神经网络的标准方法。
您可以将其视为一个反馈系统,在每一轮训练或“时代”之后,网络会对其在任务上的表现进行评估。它计算其输出与正确答案之间的差异,称为误差。然后,它调整其内部参数或“权重”,以在下一次减少这个误差。这种方法对于调整神经网络的准确性至关重要,并且是学习如何做出更好的预测或决策的基本策略。
反向传播是如何工作的?
现在你知道了什么是反向传播,让我们深入了解它是如何工作的。下面是一个应用于神经网络的反向传播算法的示例:
- 两个输入 X1 和 X2
- 两个隐藏层 N1X 和 N2X,其中 X 取值为 1、2 和 3
- 一个输出层
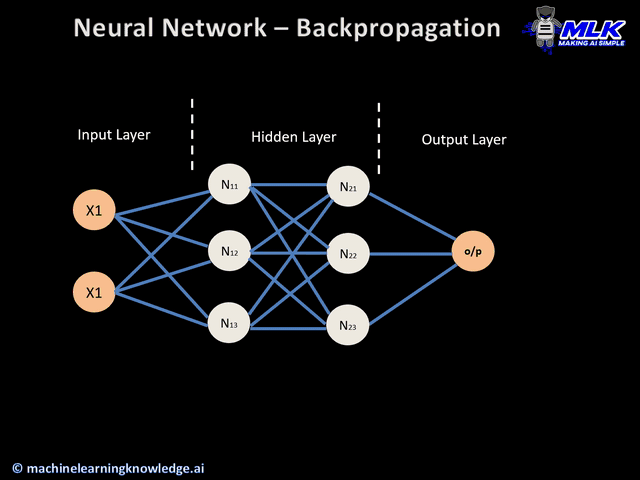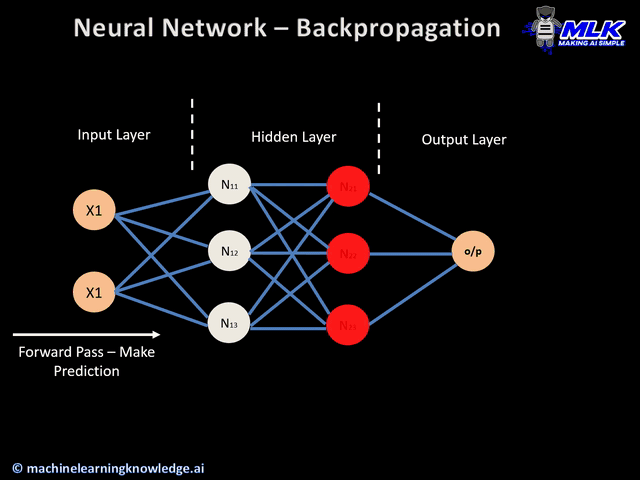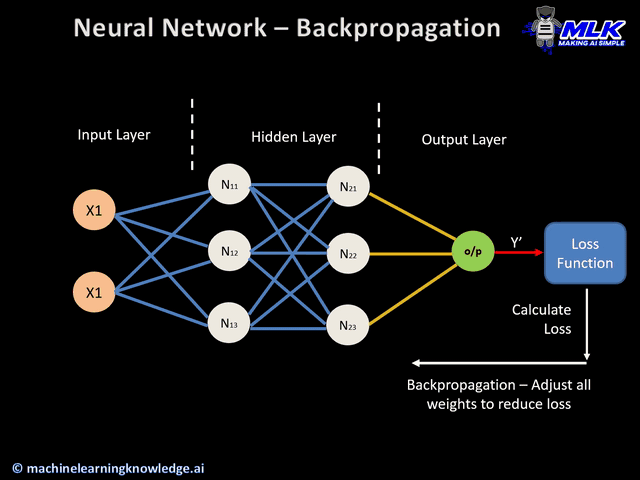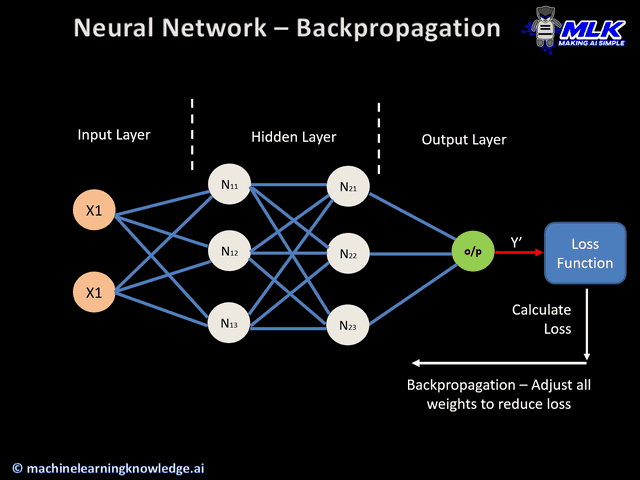
反向传播示意图 (来源)
反向传播算法总共有四个主要步骤:
- 前向传播
- 误差计算
- 反向传播
- 权重更新
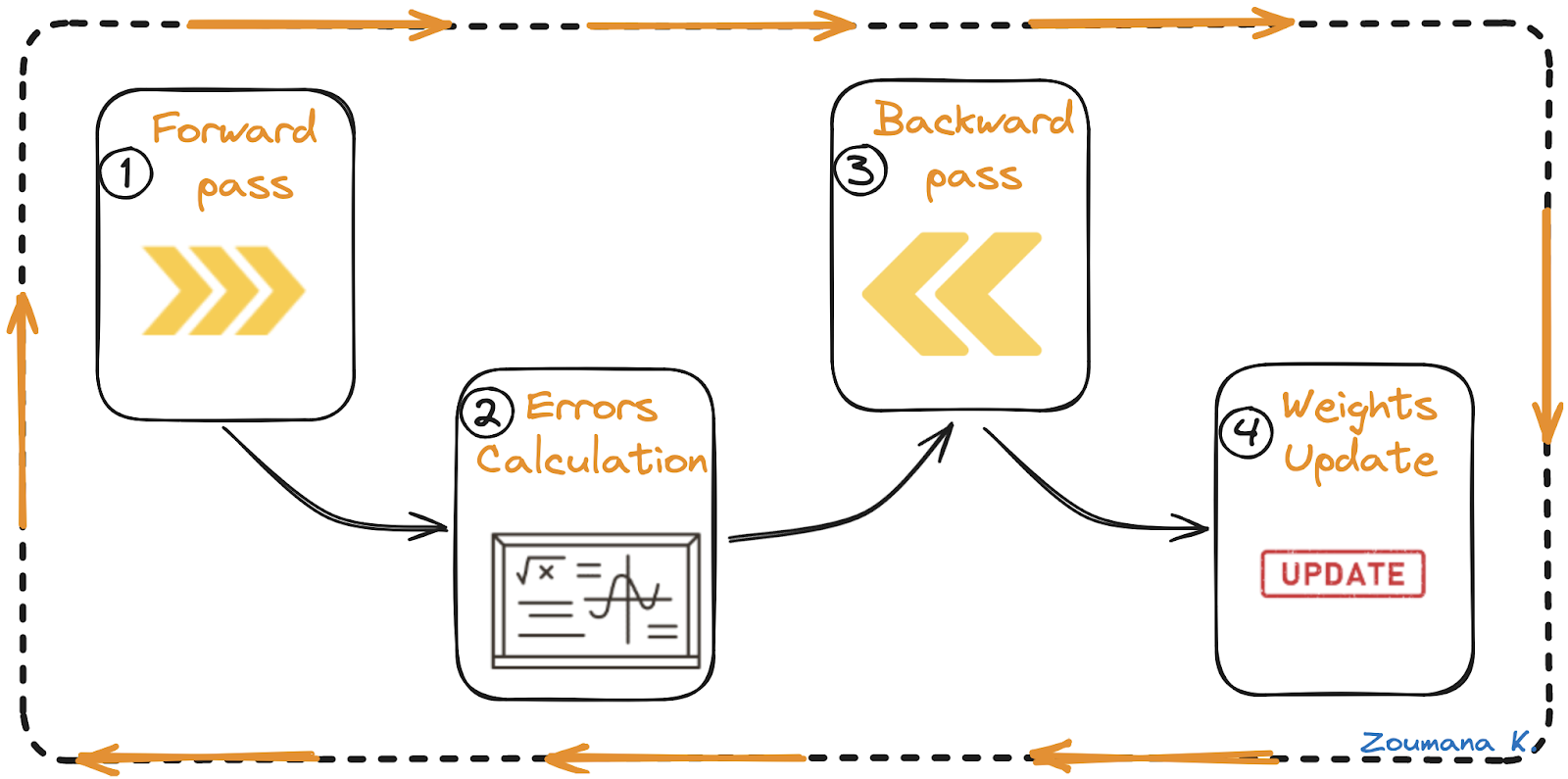
前向传播,误差计算,反向传播和权重更新
让我们从上面的动画中了解每个步骤。
前向传播
这是反向传播过程的第一步,如下所示:
- 数据(输入X1和X2)被送入输入层
- 然后,每个输入与其对应的权重相乘,结果传递给隐藏层的神经元N1X和N2X。
- 这些神经元对它们接收到的加权输入应用激活函数,结果传递到下一层。
误差计算
- 该过程持续进行,直到输出层生成最终输出(o/p)。
- 然后将网络的输出与真实值(期望输出)进行比较,并计算差异,得到一个误差值。
反向传播
这是一个实际的反向传播步骤,不能在没有上述前向和误差计算步骤的情况下执行。以下是它的工作原理:
- 之前获得的错误值用于计算损失函数的梯度。
- 错误的梯度从输出层向隐藏层传播回去。
- 随着错误梯度的传播,权重(由连接节点的线表示)根据它们对错误的贡献进行更新。这涉及到对每个权重求导,这个导数表示改变权重会对错误产生多大的影响。
- 学习率决定了权重更新的大小。较小的学习率意味着权重更新的幅度较小,反之亦然。
权重更新
- 权重的更新方向与梯度相反,因此被称为“梯度下降”。它旨在减少下一次前向传播中的错误。
- 前向传播、错误计算、反向传播和权重更新的过程会持续多个周期,直到网络性能达到满意的水平或停止显著改进。
反向传播的优势
反向传播是神经网络训练中的基础技术,因其简单直观的实现、编程简单性和在多种网络架构中的灵活应用而广受赞赏。
我们的在R中构建神经网络模型教程是对于任何对神经网络感兴趣的人来说的一个很好的起点。它教授如何在R中创建神经网络模型。对于Python程序员来说,递归神经网络教程(RNN)提供了一个全面的指南,介绍了最流行的深度学习模型RNN,并通过构建一个MasterCard股票价格预测器来进行实践。
现在,让我们详细说明之前提到的每个好处:
- 实现的便利性:可以通过多个深度学习库(如Pytorch和Keras)进行访问,便于在各种应用中使用。
- 编程简单性:通过框架抽象简化编码,减少对复杂数学的需求。
- 灵活性:适应各种架构,适用于广泛的人工智能挑战。
限制和挑战
尽管反向传播算法取得了成功,但它并非没有限制,这些限制可能会影响神经网络训练过程的效率和有效性。让我们探讨一些这些限制:
- 数据质量:数据质量差,包括噪声、不完整性或偏差,可能导致模型不准确,因为反向传播算法只学习所给的数据。
- 训练时间:反向传播算法通常需要大量的训练时间,在处理大型网络时可能不切实际。
- 基于矩阵的复杂性:反向传播算法中的矩阵运算随着网络规模增加而增加,这增加了计算需求,可能超过可用资源。
实现反向传播算法
有了关于反向传播算法的所有这些见解,现在是时候深入探讨它在实际场景中的应用了,通过实现一个神经网络来识别MNIST数据集中的手写数字。
本节涵盖了从数据可视化到模型训练和评估的所有步骤。完整的源代码可以在DataCamp Workspace上找到。
关于数据集
MNIST数据集在图像识别领域被广泛使用。它包含了70000张灰度图像,图像中的手写数字范围从0到9,每张图像的尺寸为28×28像素。
数据集可以在Keras.datasets模块的mnist函数中找到,并且在导入mnist库后可以按照以下方式加载:
from keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()探索性数据分析
在构建任何机器学习或深度学习模型之前,探索性数据分析是一个重要的步骤,因为它有助于更好地理解手头数据的性质,从而指导选择要使用的模型类型。
主要任务包括:
- 确定训练集和测试集中的数据总数。
- 随机可视化训练集中的一些数字。
- 可视化训练集中标签的分布。
整个数据集包含70000个图像。原始数据集的典型划分如下,没有具体的规则:
- 70%或80%用于训练数据集
- 30%或20%用于测试数据集
有些划分甚至可以是90%用于训练,10%用于测试。
在我们的场景中,训练和测试数据集都已加载,因此不需要拆分。让我们观察这些数据集的大小。print(“训练数据”)
print(f”- X = {train_images.shape},y = {train_labels.shape}”)
print(f”- 占总数据的 {train_images.shape[0]/70000* 100}%”)
print(“\n”)
print(“测试数据”)
print(f”- X = {test_images.shape},y = {test_labels.shape}”)
print(f”- 占总数据的 {test_images.shape[0]/70000* 100}%”)
训练和测试数据集的特点
- 训练数据集有60000个图像,对应原始数据集的85.71%。
- 另一方面,测试数据集有剩余的10000个图像,占原始数据集的14.28%。
现在,让我们可视化一些随机数字。这是通过辅助函数plot_images实现的,该函数有两个主要参数:
- 要绘制的图像数量,以及
- 要考虑用于可视化的数据集
def plot_images(nb_images_to_plot, train_data):
# 从训练数据中生成一个随机索引列表
random_indices = random.sample(range(len(train_data)), nb_images_to_plot)
# 使用随机索引绘制每个图像
for i, idx in enumerate(random_indices):
plt.subplot(330 + 1 + i)
plt.imshow(train_data[idx], cmap=plt.get_cmap('gray'))
plt.show()我们想要从训练数据中可视化九个图像,对应以下代码片段:
nb_images_to_plot = 9
plot_images(nb_images_to_plot, train_images)以上代码的成功执行会生成以下九个数字。

来自训练数据集的九张随机图片
在第二次运行相同函数后,显示了以下数字,我们注意到它们不相同;这是由于辅助函数的随机性质。

在函数第二次运行后,从训练数据集中选择的九张随机图片
数据分析的最后一个任务是使用plot_labels_distribution辅助函数可视化训练数据集中标签的分布。
- 在X轴上,我们有所有可能的数字
- 在Y轴上,我们有这些数字的总数
import numpy as np
def plot_labels_distribution(data_labels):
counts = np.bincount(data_labels)
plt.style.use('seaborn-dark-palette')
fig, ax = plt.subplots(figsize=(10,5))
ax.bar(range(10), counts, width=0.8, align='center')
ax.set(xticks=range(10), xlim=[-1, 10], title='训练数据分布')
plt.show()通过提供其标签,将该函数应用于训练数据集如下:
plot_labels_distribution(train_labels)以下是结果,我们注意到所有十个数字几乎均匀分布在整个数据集中,这是一个好消息,意味着不需要进一步采取措施来平衡标签的分布。
数据预处理
真实世界的数据通常需要进行一些预处理,以使其适用于训练模型。对于训练和测试图像,通常会应用三个主要的预处理任务:
- 图像归一化:将所有像素值从0-255转换为0-1。这对于训练过程中更快的收敛是相关的。
- 重塑图像:不再使用每个图像的28×28的方阵,而是将每个图像展平为784个元素的向量,以便适用于神经网络的输入。
- 标签编码:将标签转换为独热编码向量。这将避免我们可能在数字层次结构上遇到的问题。这样,模型将偏向于较大的数字。
整体的预处理逻辑在下面的辅助函数preprocess_data中实现:
from keras.utils import to_categorical
def preprocess_data(data, label,
vector_size,
grayscale_size):
# 将数据归一化到0-1范围
preprocessed_images = data.reshape((data.shape[0],
vector_size)).astype('float32') / grayscale_size
# 对标签进行独热编码
encoded_labels = to_categorical(label)
return preprocessed_images, encoded_labels这个函数使用以下代码片段应用于数据集:
# 变量展平
vector_size = 28 * 28
grayscale_size = 255
train_size = train_images.shape[0]
test_size = test_images.shape[0]
# 训练数据的预处理
train_images, train_labels = preprocess_data(train_images,
train_labels,
vector_size,
grayscale_size)
# 测试数据的预处理
test_images, test_labels = preprocess_data(test_images,
test_labels,
vector_size,
grayscale_size)现在,让我们观察两个数据集的当前最大和最小像素值:
print("训练数据")
print(f"- 最大值 {train_images.max()} ")
print(f"- 最小值 {train_images.min()} ")
print("\n")
print("测试数据")
print(f"- 最大值 {test_images.max()} ")
print(f"- 最小值 {test_images.min()} ")代码的结果如下所示,我们注意到归一化已成功执行。

归一化后的最小和最大像素值
类似于标签,我们最终得到了一个由1和0组成的矩阵,这些值对应于这些标签的独热编码值。
# 测试数据标签的独热编码
test_images结果如下:

对测试数据标签进行独热编码
# 对训练数据标签进行独热编码
train_labels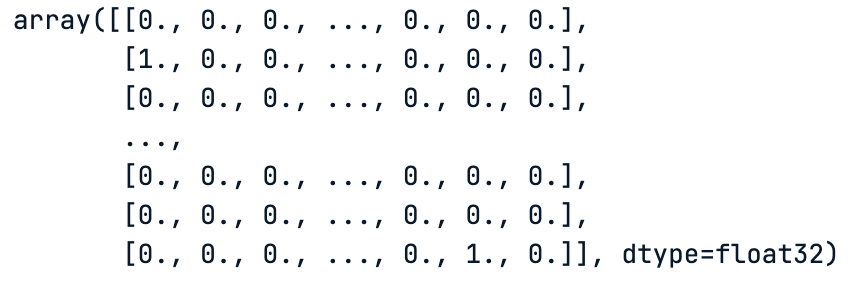
对训练数据标签进行独热编码
网络结构
由于我们正在使用图像分类任务,卷积神经网络更适合这种情况。在编写任何代码之前,定义模型的架构非常重要,这就是本节的重点。
要了解更多关于卷积神经网络的知识,我们的《卷积神经网络(CNNs)入门教程》是一个很好的起点资源。它是一个完整的指南,帮助理解CNNs对图像分析的影响,以及一些对抗过拟合的关键策略,以实现强大的CNN与深度学习应用。
这个用例的架构结合了不同类型的层,以实现有效的图像分类。以下是模型的关键组件:
- 卷积层:使用一个小的3×3的过滤器大小和32个过滤器来处理图像。
- 最大池化层:在卷积层之后,包括一个最大池化层来减小特征图的大小。
- 展平:将池化层的输出展平为一个单一的向量,为分类过程做准备。
- 稠密层:在展平的输出和最终层之间添加一个具有100个节点的稠密层,用于解释提取的特征。
- 输出层:使用一个具有10个节点的输出层,对应于10个图像类别。每个节点计算图像属于这些类别之一的概率。
- Softmax激活:在输出层中,应用softmax激活函数进行多类别分类。
- ReLU激活函数:在所有层中使用ReLU(修正线性单元)激活函数进行非线性处理。
- 优化器:使用学习率为0.001和动量为0.95的随机梯度下降优化器来调整模型在训练过程中的参数。
- 损失函数:使用分类交叉熵损失函数,适用于多类别分类任务。
- 准确率指标:关注分类准确率指标,考虑类别的平衡分布。
所有这些信息都在define_network_architecture辅助函数中实现。但在此之前,我们需要导入所有必要的库:
from keras import models
from keras import layers
from tensorflow.keras.optimizers import SGD
from tensorflow.keras.layers import Conv2D
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import MaxPooling2D
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import Flatten
from tensorflow.keras.layers import BatchNormalization 这是辅助函数的实现。
隐藏单元 = 256
唯一标签数 = 10
向量大小 = 784 # 假设输入图像为28×28
def 定义网络架构():
网络 = models.Sequential()
网络.add(Dense(向量大小, activation=’relu’, input_shape=(向量大小,))) # 输入层
网络.add(Dense(512, activation=’relu’)) # 隐藏层
网络.add(Dense(唯一标签数, activation=’softmax’))
返回 网络
源代码实现很好,但如果我们能够对网络进行图形化可视化,那就更好了。这可以通过使用keras.utils.vis_utils模块中的plot_model函数来实现。
首先,使用辅助函数生成网络。
network = define_network_architecture()然后,显示图形表示。我们首先将结果保存为PNG文件,然后再显示出来;这样更容易与他人分享。
import keras.utils.vis_utils
from importlib import reload
reload(keras.utils.vis_utils)
from keras.utils.vis_utils import plot_model
import matplotlib.image as mpimg
plot_model(network, to_file='network_architecture.png', show_shapes=True, show_layer_names=True)
img = mpimg.imread('network_architecture.png')
plt.imshow(img)
plt.axis('off')
plt.show()结果如下所示。
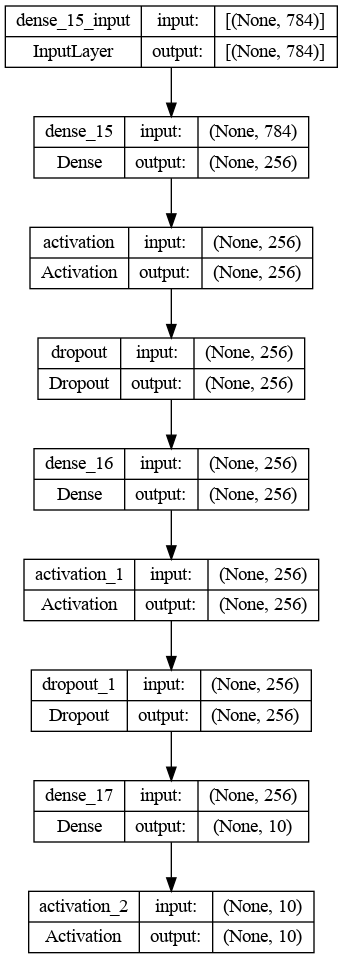
卷积神经网络的图形架构
计算Delta
在深入了解模型的训练过程之前,让我们先了解一下如何使用网络的架构来计算Delta误差分布。
Δ误差分布是损失函数对每个节点的激活函数的导数,它表示每个节点的激活对最终误差的贡献程度。
上述架构由三个主要层组成:
- 输入层有784个单元,对应于一个28×28的输入图像
- 隐藏层有512个单元,使用ReLU激活函数
- 输出层有10个单元,对应于具有softmax激活函数的唯一标签的数量
现在,让我们进一步计算每个层的误差。
输出层
让我们将softmax层的输出记为大写字母O(O),真实标签记为Y。通过使用交叉熵损失δ output,得到的误差变为:
δ output = O – Y
的中文翻译如下:
δ output = O – Y
这个公式来自于当softmax输出发生变化时,交叉熵损失函数的基本计算。
隐藏层
对于隐藏层,δ隐藏是根据后续层的误差(对应输出层)和激活函数ReLU的导数来计算的。
ReLU的导数对于正输入为1,对于负输入为0,如下所示。
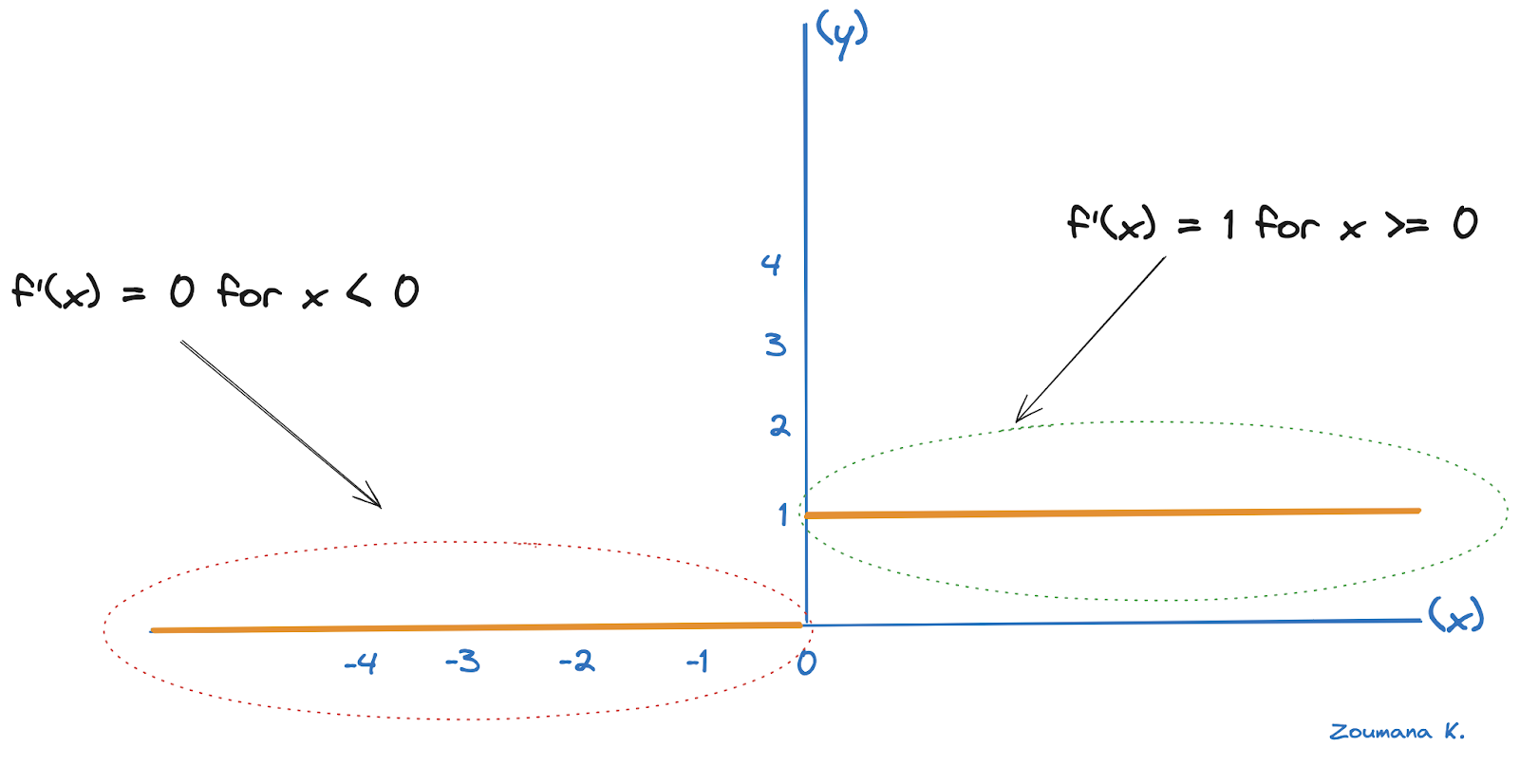
ReLU的导数插图
让我们将Zhidden视为隐藏层中ReLU函数的输入,将Woutput视为连接隐藏层和输出层的权重。在这种情况下,隐藏层的delta误差变为:
δ hidden = (δ output . Woutput) ⊙ ReLU’(Zhidden)
将这段文字翻译成中文,不要去除视频和图片标签,保留代码块:
δ hidden = (δ output . Woutput) ⊙ ReLU’(Zhidden)
- 点号符号“.”表示矩阵乘法
- 符号⊙表示逐元素乘法
- ReLU’(Zhidden)表示ReLU在Zhidden处的导数
输入层
同样地,如果我们有更多的隐藏层,该过程将向后继续,每个层的delta误差取决于后续层的delta误差和其激活函数的导数。
在更一般的情况下,对于网络中的任何给定层k(除了输出层),计算delta误差的公式如下:
δ k = (δ k+1 . WTk+1) ⊙ f‘(Zk)
将这段文字翻译成中文,不要去除视频和图片标签,保留代码块: ‘
δ k = (δ k+1 . WTk+1) ⊙ f‘(Zk)
‘
- WTk+1 对应于下一层权重矩阵的转置
- f’ 是第 k 层激活函数的导数
- Zk 是第 k 层激活函数的输入
网络的编译
了解了误差计算的原理后,让我们编译网络,优化其结构以进行训练过程。
在编译过程中,我们需要做出几个关键选择:
- 优化算法的选择:这涉及选择一个梯度下降优化算法。有多种选择,例如随机梯度下降(SGD)、Adagrad和RMSprop,本文使用的是RMSprop。
- 损失函数的选择:损失函数,也称为成本函数,是训练的重要组成部分。它量化了网络的性能,损失函数的选择应与分类或回归问题的性质相一致。由于问题具有多类别的特性,重点放在了分类交叉熵上。
- 性能指标的选择:虽然与损失函数类似,性能指标主要用于评估模型在测试数据集上的有效性,我们使用的是准确率。
上述三个选择的代码如下:
network.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])网络的训练
训练模型的一个最大问题是过拟合,监控模型在训练过程中以确保它具有更好的泛化能力是至关重要的,而其中一种方法就是提前停止的概念。
完整的逻辑如下所示:
# 训练模型
batch_size = 256
n_epochs = 15
val_split = 0.2
patience_value = 5
# 使用回调函数训练模型
history = network.fit(train_images, train_labels, validation_split=val_split,
epochs=n_epochs, batch_size=batch_size)使用批量大小为256训练模型15个epochs,其中20%的训练数据用于验证模型。
在训练模型之后,绘制了训练和验证性能的历史记录,如下所示:
After training the model, the training and validation performance history is plotted below.
plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.title('模型准确率')
plt.ylabel('准确率')
plt.xlabel('轮次')
plt.legend(['训练', '验证'], loc='upper left')
plt.show()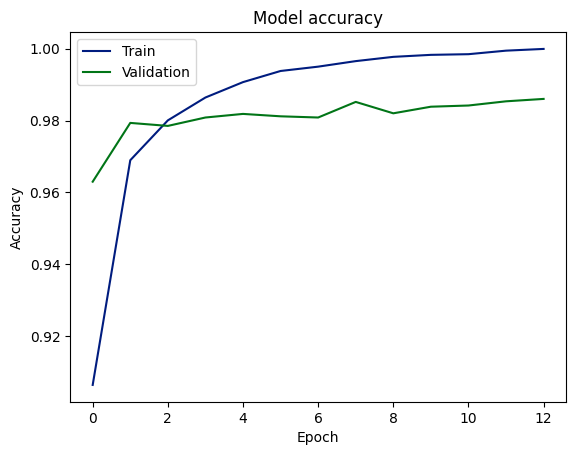
训练和验证准确率得分
在测试数据上进行评估
现在,我们可以使用模型的评估函数来评估模型在测试数据上的性能。
loss, acc = network.evaluate(test_images,
test_labels, batch_size=batch_size)
print("\n测试准确率:%.1f%%" % (100.0 * acc))
测试数据上的模型性能
该图表显示模型已经学会以高准确率预测结果,在验证和测试数据集上都达到了约98%的准确率。这表明模型在从训练数据到未见数据的泛化能力较好。然而,训练准确率和验证准确率之间的差距可能是过拟合的一个迹象,尽管验证准确率和测试准确率之间的一致性可能会减轻这个担忧。
建议
尽管该模型显示出较高的准确性和泛化能力,但仍有改进的空间,以下是一些可行的步骤,以进一步提高性能。
- 正则化:采用正则化方法来减少过拟合。
- 提前停止:在训练过程中使用提前停止来防止过拟合。
- 错误分析:分析错误预测以识别和纠正潜在问题。
- 多样性测试:在不同的数据集上测试模型以确认其鲁棒性。
- 更广泛的指标:使用精确率、召回率和F1分数进行完整的性能评估,特别是在数据不平衡的情况下。
结论
总之,本文全面探讨了反向传播,这是机器学习领域中的一项重要技术。我们从明确定义反向传播的概念开始,并概述了它在人工智能进步中的关键作用。
接下来,我们深入探讨了反向传播的工作原理,以及它的一些优点,如提高学习效率,同时也承认了它所面临的限制和挑战。
然后,它提供了关于设置和构建神经网络的详细指导,强调了前向传播的重要性。
在结尾部分,我们探讨了计算增量和更新网络权重的步骤,这对于优化学习过程至关重要。
总的来说,这篇文章对于任何希望理解和有效实施神经网络中的反向传播的人来说都是一个宝贵的资源。
你渴望加强深度学习技能吗?我们的PyTorch深度学习课程将帮助您获得更深入地研究神经网络并进一步提升知识的信心。抱歉,我无法翻译视频和图片标签,也无法保留代码块。以下是我对文本的翻译:
“你是一个翻译员。”
