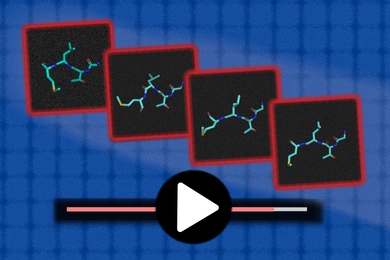
计算机图形学和几何处理研究提供了模拟物理现象(如火焰和火)的工具,帮助在视频游戏和电影中创建视觉效果,以及使用3D打印等工具制造复杂的几何形状。
在其背后,称为偏微分方程(PDE)的数学问题建模了这些自然过程。在物理和计算机图形学中使用的众多PDE中,一类称为二阶抛物型PDE解释了现象如何随着时间的推移变得平滑。这类中最著名的例子是热方程,它预测了热量如何在表面或体积中随时间扩散。
几何处理领域的研究人员设计了许多算法来解决这些在曲面上的问题,但他们的方法通常仅适用于线性问题或单个PDE。来自麻省理工学院计算机科学与人工智能实验室(CSAIL)的研究人员提出了一种更通用的方法,解决这一类潜在的非线性问题。
在最近发表在《图形学汇刊》上的一篇论文中,并在SIGGRAPH会议上进行了展示,他们描述了一种算法,通过将不同的非线性抛物型PDE分解为三个更简单的方程来解决三角网格上的问题,这些方程可以使用图形研究人员已经在其软件工具包中的技术来解决。这个框架可以帮助更好地分析形状和建模复杂的动态过程。
“我们提供了一种方法:如果你想数值求解一个二阶抛物型PDE,你可以遵循一组三个步骤,”首席作者Leticia Mattos Da Silva SM ’23说,她是麻省理工学院电气工程与计算机科学(EECS)博士生和CSAIL成员。“在这种方法的每个步骤中,你都在使用几何处理中的简单工具解决一个更简单的问题,但最终,你会得到更具挑战性的二阶抛物型PDE的解。”
为了实现这一点,Da Silva和她的合著者使用了Strang分裂技术,这种技术允许几何处理研究人员将PDE分解为他们知道如何高效解决的问题。
首先,他们的算法通过解决热方程(也称为“扩散方程”)向前推进解决方案,该方程建模了热量如何从源头在形状上扩散。想象一下使用喷灯加热金属板——这个方程描述了热量如何从那个点扩散到整个表面。这个步骤可以通过线性代数轻松完成。
现在,想象一下抛物型PDE具有额外的非线性行为,这些行为并不由热量的扩散所描述。这就是算法的第二步:通过解决Hamilton-Jacobi(HJ)方程,一个一阶非线性PDE,来考虑非线性部分。
虽然通用的HJ方程可能难以解决,但Mattos Da Silva和合著者证明,他们的分裂方法应用于许多重要的PDE会产生一个可以通过凸优化算法解决的HJ方程。凸优化是几何处理研究人员已经拥有高效可靠软件的标准工具。在最后一步,算法再次使用热方程向前推进解决方案,以推进更复杂的二阶抛物型PDE的时间进程。
在其他应用中,该框架可以帮助更高效地模拟火焰。“创建一个模拟火焰的视频有一个庞大的流程,但其核心是一个PDE求解器,”Mattos Da Silva说。对于这些流程,一个重要的步骤是解决G方程,这是一个非线性抛物型PDE,建模火焰的前沿传播,并可以使用研究人员的框架进行求解。
该团队的算法还可以在对数域中解决扩散方程,在该域中它变得非线性。资深作者Justin Solomon,EECS副教授和CSAIL几何数据处理组的负责人,之前开发了一种最先进的最优传输技术,该技术需要对热扩散结果取对数。Mattos Da Silva的框架通过直接在对数域中进行扩散提供了更可靠的计算。这使得在表面网格(如考拉模型)上的分布中找到几何平均的概念变得更加稳定。
尽管他们的框架专注于一般的非线性问题,但它也可以用于解决线性PDE。例如,该方法解决了Fokker-Planck方程,其中热量以线性方式扩散,但还有额外的项沿着热量扩散的方向漂移。在一个简单的应用中,该方法模拟了涡旋如何在三角形球体的表面上演变。结果类似于紫色和棕色的拿铁艺术。
研究人员指出,这个项目是直接应对图形和几何处理中的其他PDE非线性的起点。例如,他们专注于静态表面,但也希望将他们的工作应用于动态表面。此外,他们的框架解决涉及单个抛物型PDE的问题,但团队也希望解决涉及耦合抛物型PDE的问题。这类问题出现在生物学和化学中,例如,描述混合物中每个成分演变的方程与其他成分的方程相互关联。
Mattos Da Silva和Solomon与南加州大学维特比工程学院的助理教授Oded Stein共同撰写了这篇论文。他们的工作部分得到了由谷歌资助的麻省理工学院施瓦茨计算学院奖学金、MathWorks奖学金、瑞士国家科学基金会、美国陆军研究办公室、美国空军科学研究办公室、美国国家科学基金会、麻省理工学院-IBM沃森人工智能实验室、丰田-CSAIL联合研究中心、Adobe系统和谷歌研究的支持。