在机器学习中的交叉熵损失函数：提高模型准确性

几乎我们今天使用的所有应用程序都包含一种形式的机器学习，以增强或自动化业务流程。

Almost all of the applications we use today incorporate a form of machine learning to enhance or automate a business process.

‘

然而，这些模型不能简单地推向实时环境 – 尤其是在高风险环境中（即，预测某人是否患癌症）。在进入生产之前，它们必须经过优化，以便高效有效地运行。这意味着必须对模型参数进行微调，以确保它们对改善客户体验起到积极作用。

在训练过程中，从业者通常使用损失/成本函数来寻找机器学习模型的最优解。交叉熵是最常用的损失函数之一，用于优化分类模型。你可以在这里了解更多关于损失函数的内容，以及在这里了解更多关于分类模型的内容。

在这篇文章中，我们将深入探讨以下内容：

  • 什么是交叉熵？
  • 计算交叉熵
  • 交叉熵作为损失函数
  • 最佳实践。

理解熵

交叉熵的概念源于信息论领域，信息熵，也被称为香农熵，是由克劳德·香农在1948年的一篇名为“A Mathematical Theory of Communication”的论文中正式引入的。在我们讨论交叉熵之前，让我们先了解熵。

熵计算系统内的随机性或无序程度。在信息论的背景下，随机变量的熵是可能结果固有的平均不确定性、惊讶或信息量。简单来说，它衡量了事件的不确定性。

例如，如果抛掷一枚公平的硬币，我们将有两种可能的结果，硬币落在正面或反面的概率都是1/2。

这意味着：P(X=正面) = P(X=反面) = ½。

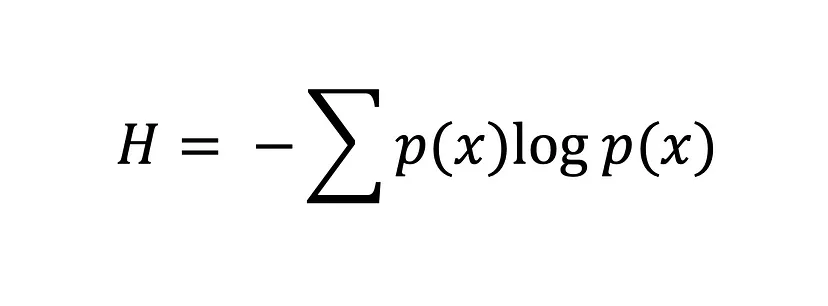
香农熵方程

香农熵方程

使用香农熵方程，硬币的两个面的熵都等于0，这意味着几乎没有任何不确定性 – 它要么几乎总是正面，要么几乎总是反面。

熵的值越大，H(x)，概率分布的不确定性就越大，而值越小，不确定性就越小。

现在，我们准备深入研究交叉熵。

什么是交叉熵？

交叉熵，也被称为对数损失或对数损失函数，是机器学习中常用的一种损失函数，用于衡量分类模型的性能。

它衡量了使用另一个概率分布q的最优编码来识别来自概率分布p的事件所需的平均比特数。换句话说，交叉熵衡量了分类模型的发现概率分布与预测值之间的差异。

交叉熵损失函数用于在训练过程中通过调整机器学习模型的权重来寻找最优解。目标是最小化实际结果与预测结果之间的误差。因此，接近0的度量是一个好模型的标志，而接近1的度量是一个性能较差的模型的标志。

如果你熟悉Kullback-Leibler（KL）散度，你可能会想，“交叉熵和KL散度有什么区别？”这是一个合理的问题。这两个概念都被广泛用于衡量概率分布的差异或相似性。尽管它们有一些相似之处，但它们的用途不同。

如上所述，交叉熵衡量了使用另一个概率分布Q的最优编码来识别来自概率分布P的事件所需的平均比特数，并且通常用于机器学习中评估模型的性能，其中目标是最小化预测概率分布与真实分布之间的误差。相比之下，KL散度衡量了两个概率分布P和Q之间的差异。换句话说，KL散度量化了在使用Q来近似P时的信息损失量。这在无监督学习任务中非常有用，其目标是通过最小化真实数据分布和学习数据分布之间的差异来揭示数据中的结构。

交叉熵作为损失函数

在机器学习中，损失函数帮助模型确定其错误程度，并根据这个错误程度进行改进。它们是数学函数，用于量化机器学习模型中预测值与实际值之间的差异，但这并不是它们的全部作用。

损失函数的误差度量也在优化过程中作为指导，通过向模型提供关于其与数据拟合程度的反馈。因此，在优化阶段，大多数机器学习模型都会实现损失函数，选择模型参数以帮助模型最小化误差并达到最优解 – 误差越小，模型越好。

我们可以使用交叉熵损失函数来衡量两个概率分布之间的误差。例如，假设我们正在进行一个二元分类任务（一个包含两个类别0和1的分类任务）。

在这种情况下，我们必须使用二进制交叉熵，这是所有数据样本的平均交叉熵：

二进制交叉熵公式。[来源：交叉熵损失函数]

二进制交叉熵公式 [来源：交叉熵损失函数]

如果我们要计算一个正确值为y=1的单个数据点的损失，我们的方程将如下所示：

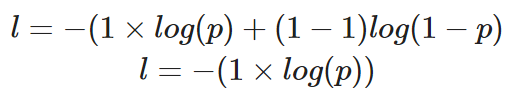
计算二进制交叉熵，其中真实值为1的单个实例

计算二进制交叉熵，其中真实值为1的单个实例

预测概率p决定了损失值l的数值。如果p的值很高，模型将因为做出正确的预测而受到奖励 – 这将通过一个较低的损失值l来说明。

然而，一个较低的预测概率p会推断模型是错误的，而二元交叉熵损失函数将通过使l的值更高来反映这一点。

对于多类分类任务，交叉熵（或常常被称为分类交叉熵）可以简单地扩展如下：

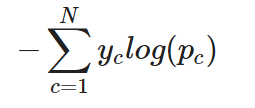
单个实例的分类交叉熵

单个实例的分类交叉熵

换句话说，对于多类分类任务，交叉熵会分别计算每个类别的损失，然后将其相加以确定总损失。

在本教程的这一部分中，我们将学习如何在PyTorch和TensorFlow中使用交叉熵损失函数。

在PyTorch和TensorFlow中实现交叉熵损失

在本教程的这一部分中，我们将学习如何在TensorFlow和PyTorch中使用交叉熵损失函数。

让我们从创建数据集开始。我们将使用Scikit-learn的make_classification函数来帮助我们：

“`python
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split

# 创建训练数据
X, y = make_classification(
n_samples=10000,
n_informative=10,
random_state=2022
)

# 分割为训练集和测试集
X_new, X_test = X[:9000, :], X[9000:, ]
y_new, y_test = y[:9000], y[9000:]

X_train, X_val, y_train, y_val = train_test_split(
X_new, y_new,
test_size=0.3
)
print(f”训练数据: {X_train.shape}\n\
训练标签: {y_train.shape}\n\
测试数据: {X_test.shape}\n\
测试标签: {y_test.shape}”)

“””
训练数据: (6300, 20)
训练标签: (6300,)
测试数据: (1000, 20)
测试标签: (1000,)
“””
“`

TensorFlow中的交叉熵

我们将构建的模型包括一个输入层、一个隐藏层和一个输出层。

由于这是一个二分类任务，我们将使用二元交叉熵作为我们的损失函数。

# 构建和训练模型
model = tf.keras.Sequential([
tf.keras.layers.Dense(10,
input_shape=(X_train.shape[1],),
activation=”relu”),
tf.keras.layers.Dense(10,
activation=”relu”),
tf.keras.layers.Dense(1, activation=”sigmoid”)
])

model.compile(
loss=”binary_crossentropy”, # 在这里指定损失函数
optimizer=”adam”,
metrics=[“accuracy”])

history = model.fit(X_train, y_train, epochs=20, validation_data=[X_val, y_val], verbose=0)

接下来，我们将绘制损失图，以查看模型是否在改善 – 即每个时期的误差是否减少，直到无法再改善为止。

# 绘制模型的损失
fig, ax = plt.subplots(figsize=(8,5))
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('模型损失')
plt.ylabel('损失')
plt.xlabel('轮次')
plt.xticks(np.arange(0,20, step=1))
plt.legend(['训练', '测试'], loc='upper right')
plt.show()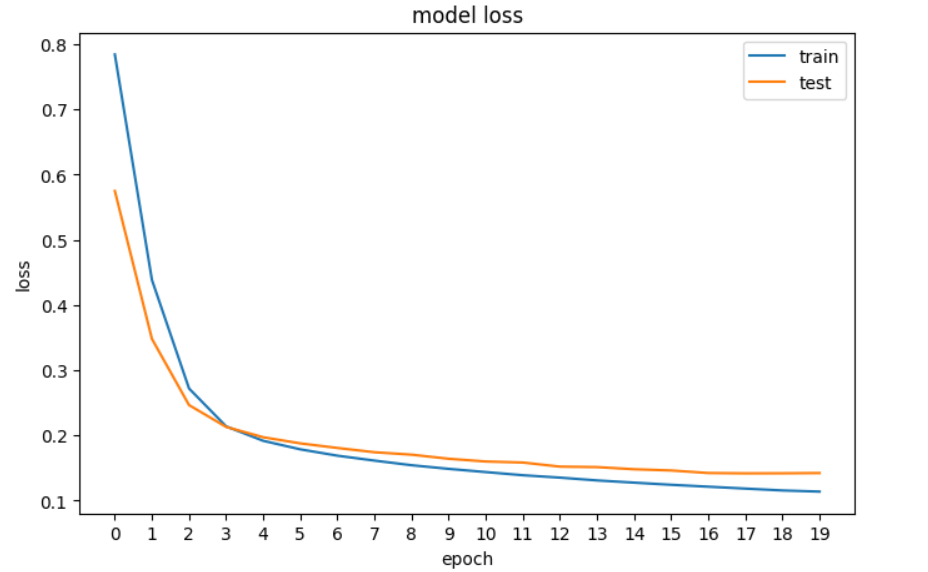

我们在TensorFlow中神经网络的损失图

我们在TensorFlow中神经网络的损失图。

PyTorch中的交叉熵

在PyTorch中，模型的输入、输出和参数都使用张量进行编码，这意味着我们必须将我们的Numpy数组转换为张量。这是下面代码中我们要做的第一件事，然后我们构建神经网络并打印其维度。

# 将numpy数组转换为张量
X_train_tensor = torch.tensor(X_train, dtype=torch.float32)
X_val_tensor = torch.tensor(X_val, dtype=torch.float32)
y_train_tensor = torch.tensor(y_train, dtype=torch.float32).reshape(-1, 1)
y_val_tensor = torch.tensor(y_val, dtype=torch.float32).reshape(-1, 1)

# 构建模型
input_dim = X_train.shape[1]
hidden_dim = 10
output_dim = 1

model = nn.Sequential(
    nn.Linear(input_dim, hidden_dim),
    nn.ReLU(),
    nn.Linear(hidden_dim, hidden_dim),
    nn.ReLU(),
    nn.Linear(hidden_dim, output_dim),
    nn.Sigmoid()
    )

print(model)

"""
Sequential(
  (0): Linear(in_features=20, out_features=10, bias=True)
  (1): ReLU()
  (2): Linear(in_features=10, out_features=10, bias=True)
  (3): ReLU()
  (4): Linear(in_features=10, out_features=1, bias=True)
  (5): Sigmoid()
)
"""

接下来，我们定义二元交叉熵损失函数和优化器：

loss_fn = nn.BCELoss() # 二元交叉熵
optimizer = optim.Adam(model.parameters(), lr=0.001)
现在来绘制损失函数：# 绘制模型的损失
fig, ax = plt.subplots(figsize=(8,5))
plt.plot(train_loss)
plt.plot(val_loss)
plt.title(‘模型损失’)
plt.ylabel(‘损失’)
plt.xlabel(‘轮次’)
plt.xticks(np.arange(0,20, step=1))
plt.legend([‘训练’, ‘测试’], loc=’upper right’)
plt.show()

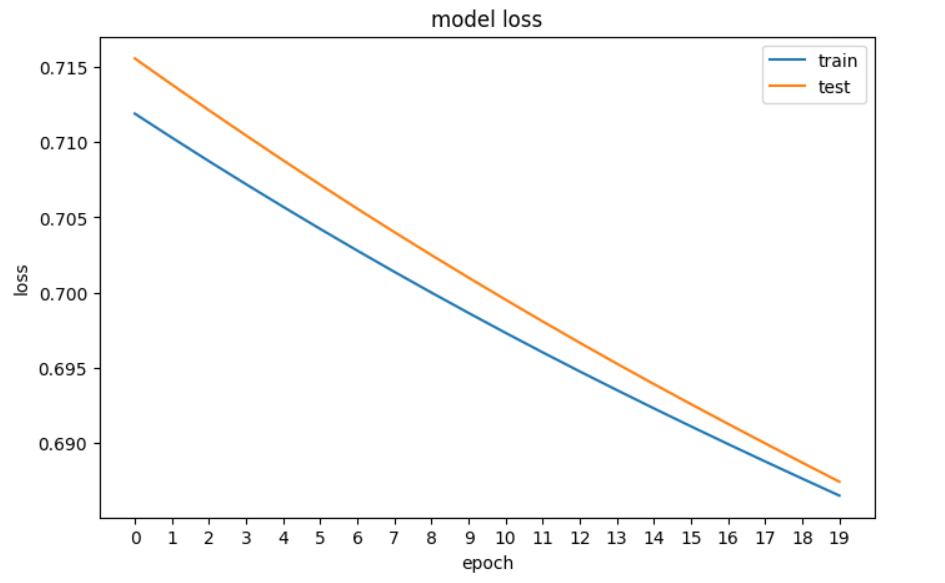
![神经网络在PyTorch中的损失图](https://images.datacamp.com/image/upload/v1704977342/image2_021a65ce00.png)

我们在PyTorch中的神经网络损失的绘图

主要要点

以下是我们对交叉熵损失的学习内容的快速回顾：

  • 熵计算系统内的随机性或无序程度，以衡量事件的不确定性。如果结果是确定的，熵的度量将会很低。
  • 交叉熵，也称为对数损失或对数损失，是机器学习中常用的损失函数，用于衡量分类模型的性能。它衡量了分类模型发现的概率分布与预测值之间的差异。
  • 二元交叉熵用于二元分类，而分类交叉熵用于多类分类。
  • 交叉熵类似于KL散度，但它们有不同的用途：交叉熵通常用于机器学习中评估模型的性能，目标是最小化预测概率分布与真实分布之间的误差，而KL散度在无监督学习任务中更有用，目标是通过最小化真实数据分布与学习数据分布之间的差异来揭示数据中的结构。

要继续学习，请查看我们的资源：

相关文章